Capítulo 12 Migração e Fluxo Gênico

A Grande Muralha da China tem servido como uma barreira física ao fluxo gênico entre subpopulações de plantas separadas por mais de 600 anos, como por exemplo para o damasqueiro tibetano (_Prunus armeniaca_), em floração. Foto: runchinamarathon.com/images (2014)

Figura 12.1: A Grande Muralha da China tem servido como uma barreira física ao fluxo gênico entre subpopulações de plantas separadas por mais de 600 anos, como por exemplo para o damasqueiro tibetano (Prunus armeniaca), em floração. Foto: runchinamarathon.com/images (2014)

Su et al. 2003. doi: 10.1038/sj.hdy.6800237

12.1 Migração $\times$ Fluxo gênico

Como visto anteriormente, quando populações se encontram estruturadas, as subpopulações irão divergir por deriva genética.

Cabe assim à migração promover o cruzamento de indivíduos de um deme com os de outro, e logo, o fluxo de genes entre as subpopulações.

Contudo, a migração faz referência geralmente à indivíduos juvenis e adultos, e não necessariamente inclui o intercruzamento de indivíduos de populações diferentes (e. g.,, pássaros migratórios).

Enquanto o fluxo gênico requer necessariamente que haja intercruzamento, o qual é também promovido por dispersão de larvas, sementes e gametas.

Figura 12.2: A migração de indivíduos entre subpopulações promove o fluxo gênico.

Migração – O movimento de membros de uma espécie para um ambiente diferente.

Fluxo gênico – A transferência da variação genética de uma população para outra.

12.2 Modelando a migração

Conside um modelo simples onde duas populações locais trocam genes ao permutar uma proporção $m$ do total de seus indivíduos a cada geração reciprocamente.

Assim, em um lócus com dois alelos $A$ e $a$, teremos…

… na população 1:

\[f(A,Pop\ 1) = p_1\]

\[f(a,Pop\ 1) = q_1\]

… e na população 2:

\[f(A,Pop\ 2) = p_2\]

\[f(a,Pop\ 2) = q_2\]

Assim, a frequência $p'$ do alelo $A$ na próxima geração dependerá da fraçao $m$ de migrantes trocada entre as duas populações, de forma que…

… na população 1:

\[p'_1 = (1-m)p_1 + mp_2\]

… e na população 2:

\[p'_2 = (1-m)p_2 + mp_1\]

Onde $m$ é a fração de migrantes entre as duas populações, e $1-m$ é a a fração de não-migrantes.

Figura 12.3: A frequência alélica $p$ após uma geração com uma taxa de migração recíproca $m$ entre duas populações.

A mudança nas frequências gênicas promovida pelo fluxo gênico dependerá assim da fração $m$ de migrantes e da diferença prévia existente entre as frequências gênicas $p_1$ e $p_2$ das populações, de forma que…

… na população 1:

\[ \begin{aligned} \Delta p_1 &= p’_1 – p_1 \\ &= (1 – m)p_1 + mp_2 \ – \ p_1 \\ &= p_1 – mp_1 + mp_2 \ – \ p_1 \\ &= mp_2 \ – \ mp_1 \\ &= m(p_2 \ – \ p_1) \end{aligned} \]

… e na população 2:

\[ \begin{aligned} \Delta p_2 &= p’_2 – p_2 \\ &= (1 – m)p_2 + mp_1 \ – \ p_2 \\ &= p_2 – mp_2 + mp_1 \ – \ p_2 \\ &= mp_1 \ – \ mp_2 \\ &= m(p_1 \ – \ p_2) \end{aligned} \]

Desta maneira, a migração será uma força evolutiva (promeverá mudança nas frequências gênicas), quando:

$m > 0$ – i. e. , há fluxo gênico (viz., as populações locais não estão totalmente isoladas); e
$p_1 \neq p_2$ – i. e., há divergência genética entre as populações locais (o que quase sempre irá ocorrer, uma vez que as subpopulações são finitas e possuem uma história evolutiva prévia, viz., deriva genética).

Assim, quando $p_1 = 0$ e $p_2 > 0$, O fluxo gênico introduzirá nova variação genética na população 1, uma vez que $p’_1 = mp_2$

Neste sentido o fluxo gênico atuará localmente como um processo criativo, semelhante à mutação, mas mais expressivo do que esta, pois geralmente $m \gg µ$ (ver taxa de mutação em [#Mutação]).

12.3 Migração ao longo do tempo

O fluxo gênico entre populações geneticamente distintas promove mudança nas frequências gênicas (evolução).

Contudo, esta mudança ocorre em uma direção específica.

Assim, se…

…na população 1

\[ \begin{aligned} p'_1 &= (1-m)p_1 + mp_2 \\ &= p_1 - mp_1 + mp_2 \\ &= p_1 - (mp_1 - mp_2) \\ &= p_1 - m(p_1 - p_2) \end{aligned} \]

… e na população 2:
…na população 1

\[ \begin{aligned} p'_2 &= (1-m)p_2 + mp_1 \\ &= p_2 - mp_2 + mp_1 \\ &= p_2 + (mp_1 - mp_2) \\ &= p_2 + m(p_1 - p_2) \end{aligned} \]

E se chamarmos $d$ a diferença entre as frequências gênicas das duas populações em uma dada geração, de forma que:

\[ d = p_1 - p_2\]

Então teremos que:

\[p'_1 = p_1 - md\]

\[p'_2 = p_2 + md\]

Assim, a diferença entre as frequências gênicas das duas populações na geração seguinte $d'$, será:

\[ \begin{aligned} d' &= p’_1 \ – \ p’_2 \\ &= (p_1 - md) - (p_2 + md) \\ &= p_1 - md - p_2 - md \\ &= p_1 - p_2 - 2md \end{aligned} \]

Assim, se $ d = p_1 - p_2$, logo teremos que:

\[ \begin{aligned} d' &= d - 2md \\ &= d(1-2m) \end{aligned} \]

Desta forma, o fluxo gênico entre as populações, quando $m>0$, leva à redução da diferença entre as frequências alélicas das subpopulações, proporcional a taxa de migração $m$, uma vez que $d'<d$.

Logo, após $t$ gerações de migração, temos que:

\[d_t = d(1 – 2m)^t\]

Assim:

$d_t \to 0$, quando $t \to \infty$;
e $d = 0$, quando $p_1 = p_2 = 0.5$

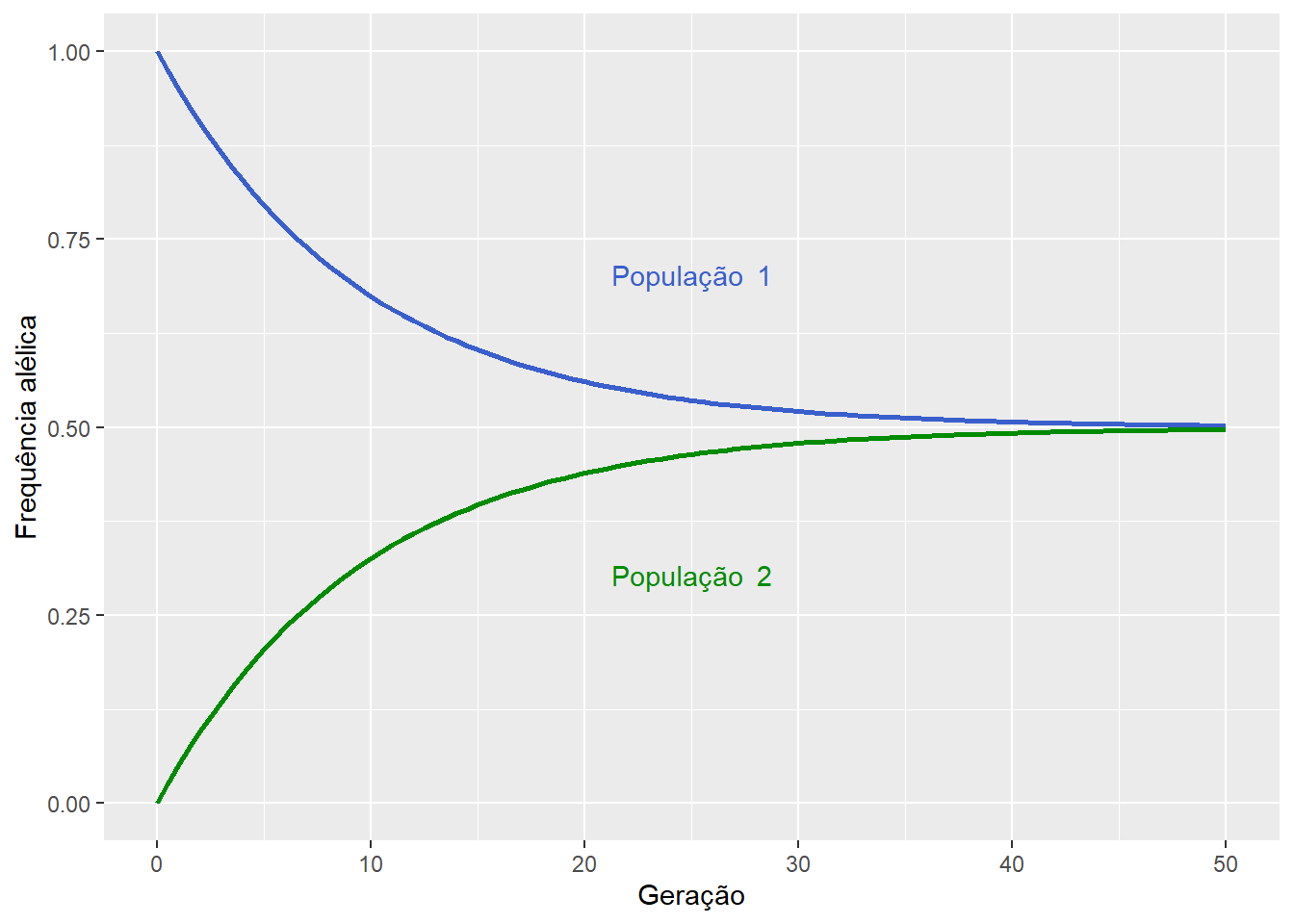
Figura 12.4: O fluxo gênico entre duas populações levará ao equilíbrio das frequências alélicas proporcionalmente a taxa de migracão $m$.

O fluxo gênico pode ser visto como o ponto que conecta as populações:

Em curto prazo, o fluxo gênico atua como uma força evolutiva criadora, pois introduz novas variantes alélicas em populações locais divergentes ou mesmo em espécies próximas por meio de hibridização e introgressão.
Em longo prazo, o fluxo gênico atua como uma força evolutiva conservadora, pois restringe a diferenciação gênica entre populações, promovendo a conectividade e mistura.

12.4 O modelo fonte-dreno

No modelo fonte-dreno, também conhecido como continentes-ilha, o fluxo gênico ocorre unidirecionalmente, a partir de uma grande população (fonte) para uma menor (dreno).

Desta forma, a introdução de alelos vindos da população fonte afeta a freqüência alélica na população dreno, mas não ao contrário.

Como a população fonte não recebe migrantes da população dreno, ou, se o faz, a diferença no tamanho das duas populações torna a fração de migrantes desprezível, teremos que a frequência $P$ do alelo $A$ não é alterada pelo fluxo gênico, e permanecerá constante de uma geração para a outra.

Contudo, na população dreno, a frequência $p$ do alelo $A$ na próxima geração será influenciada pela fração $m$ de migrantes oriundos da população fonte, de forma que:

\[p_1 = (1 – m)p_0 + mP\]

Figura 12.5: A frequência alélica $p$ após uma geração com uma taxa de migração unidirecional $m$ pa população fonte para a população dreno.

Como a frequência $P$ não muda, podemos prever que:

\[p_2 = (1 – m)p_1 + mP\]

\[p_3 = (1 – m)p_2 + mP\]

\[...\]

E assim, em termos gerais, a frequência $p$ do alelo $A$ na população dreno após $t$ gerações será:

\[p_t = (p_0 - P)(1 - m)^t+ P\]

De forma que $p_t \to P$, quando $t \to \infty$.

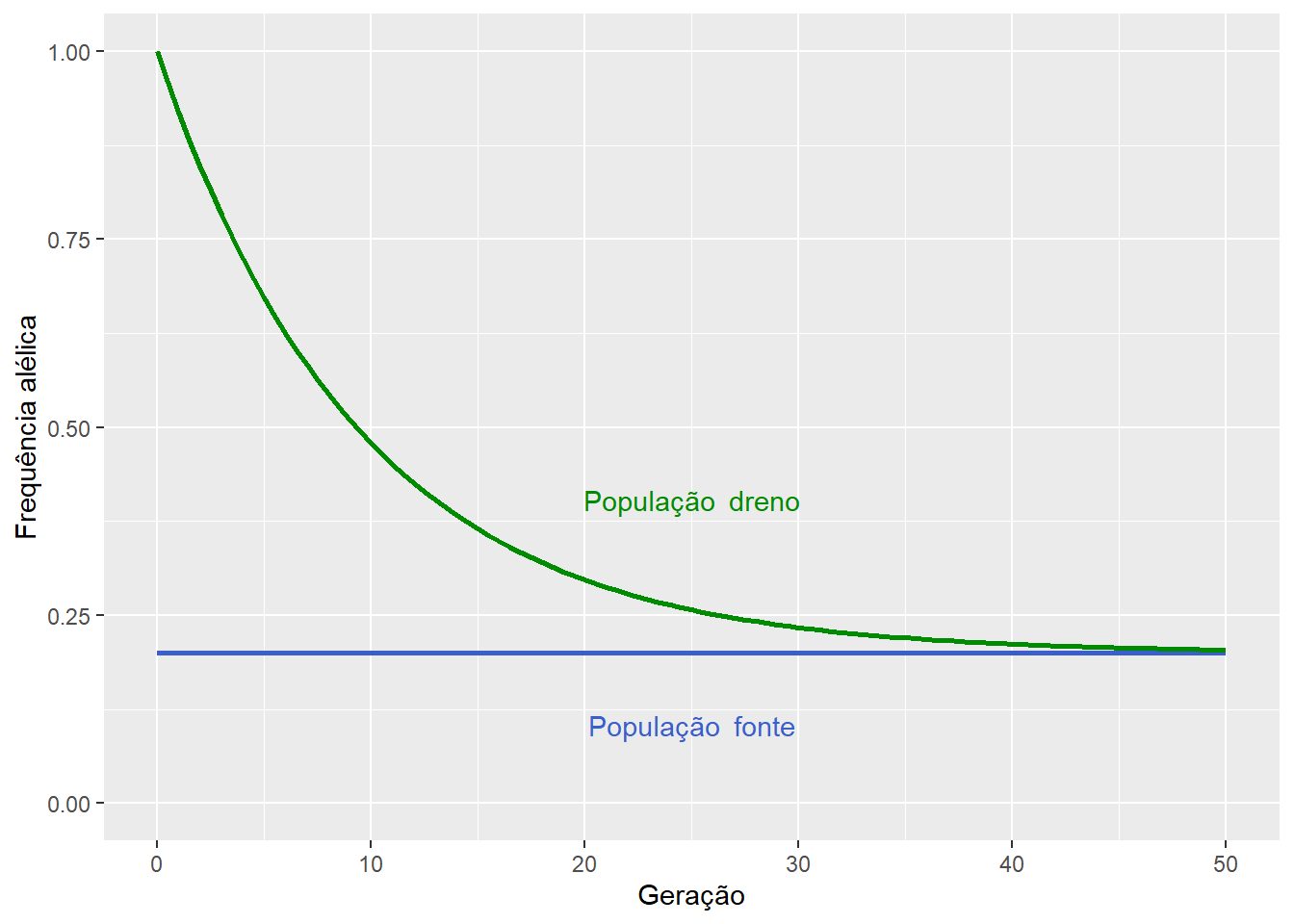
O fluxo gênico da população fonte para a população dreno promoverá, após certo tempo, dada a taxa de migracão $m$, a substituiçào dos alelos na última.

Figura 12.6: O fluxo gênico da população fonte para a população dreno promoverá, após certo tempo, dada a taxa de migracão $m$, a substituiçào dos alelos na última.

12.5 O modelo de ilhas

O modelo de ilha é uma modelagem mais complexa da migraÇão, onde todas $n$ populações estão conectadas através de uma taxa de migração $m$ constante.

A maneira mais simples de modelar esse tipo de sistema é considerar que os migrantes compreendem um grande reservatório de migrantes, que são distribuídos para todas as populações.

Se $\bar{p}$ é a frequência alélica média global, o conjunto de migrantes pode ser considerado como tendo também essa frequência alélica.

Sendo assim, a frequência $p$ do alelo $A$ na $i$-nésima população na próxima geração será:

\[p_{i,t+1} = (1-m)p_{i, t} + m\bar{p}\]

12.6 Equilíbrio entre fluxo gênico e deriva gênica

O fluxo gênico atua reduzindo a probabilidade de identidade por descendência (IBD), uma vez que um alelo introduzido de fora de uma população significa que não haverá ancestralidade comum dentro da população.

Usando o índice de fixação ($F_{ST}$) como a medida do progresso da deriva genética, i.e., como a probabilidade de identidade por descendência em subpopulações relativas à metapopulação total, podemos expressar assim probabilidade total de identidade por descendência em populações migrantes.

Como visto anteriormente, em uma dada geração $t$, o coeficiente de endogamia ($F$) será:

\[F_t = \frac{1}{2N_e} + \left( 1- \frac{1}{2N_e} \right)F_{t-1}\]

Assumindo que a migração traz genes inteiramente não relacionados de outras populações, com probabilidade $m$:

$(1 – m)$ – é a chance de que um alelo qualquer em uma geração não ter surgido por migração, e
$(1 – m)^2$ – é a chance de que nenhum dos dois alelos combinados em uma fecundação tenha imigrado nessa geração.

Assim, depois de contabilizar a possibilidade de migração, a probabilidade geral de identidade por descendência na geração tempo $t$ será:

\[F_t = \left[ \frac{1}{2N_e} + \left( 1- \frac{1}{2N_e} \right)F_{t-1} \right] \left( 1-m\right)^2\]

Como o tamanho efetivo da população $N_e$ e a taxa de migração $m$ são os dois únicos parâmetros para determinar o coeficiente de endogamia $F$ conforme acima, é bastante claro que os efeitos combinados da deriva genética e da migração devem tender a algum tipo de valor de equilíbrio.

Sendo o coeficiente de endogamia de equilíbrio $\hat{F}$, onde $\hat{F} = F_t = F_{t-1}$, teremos que:

se $N$ e $m$ são pequenos, a deriva supera a migração, e $\hat{F} \approx 1$, mas
se $N$ e $m$ são grandes, a migração irá homogeneizar as frequências dos genes mais rapidamente do que a deriva, e $\hat{F} \approx 0$.

E assim, o coeficiente de endogamia de equilíbrio $\hat{F}$ será:

\[\hat{F} = \left[ \frac{1}{2N_e} + \left( 1- \frac{1}{2N_e} \right)\hat{F} \right] \left( 1-m\right)^2\]

Assintoticamente à taxa de migração $m$, i. e., assumindo que o valor de $m$ é pequeno o suficiente para que $m^2 \sim 0$, teremos que:

\[ (1 - m)^2 \sim 1-2m\]

E assim, após várias simplificações algébricas da equação anterior (veja [aqui][#Provas]), teremos que:

\[\hat{F} \sim \frac{1-2m}{4N_em+1-2m} \]

Desde que $2m \ll Nm$ e $2m \ll 1$, teremos a relação aproximada:

\[\hat{F} \sim \frac{1}{4N_em+1} \]

Quando o índice de fixação ($F_{ST}$) é conhecido, podemos expressá-lo como:

\[F_{ST} \sim \frac{1}{4N_em+1} \]

\[N_em \sim \frac{ \frac{1}{F_{ST}}-1}{4} \]

Neste contexto, $N_em$ representa o número efetivo de migrantes em uma população.

Por esse motivo, algumas pessoas passaram a ver estimativas de $N_em$ como medidas de “fluxo gênico”, quando, na verdade, $N_em$ não mede fluxo gênico, o que é dado efetivamente pela taxa de migração $m$.

O que $N_em$ realmente irá medir é a “tendência de produzir $F_{ST}$ sob deriva aleatória”, desde que as suposições bastante irrealistas do modelo de ilha sejam cumpridas.

Assim:

Se $N_em > 1$, há fluxo gênico suficiente para negar os efeitos da deriva genética, e manter a conectividade entre as populações, mas
Se $N_em > 4$, então as populações locais podem ser consideradas pertencer a uma única população panmítica.

$O índice de fixação ($F_{ST}$) é uma função não-linear do número efetivo de migrantes ($N_em$). Ver Whitlock & McCauley ([1999](https://doi.org/10,1038/sj.hdy.6884960)).$

Figura 12.7: O índice de fixação ($F_{ST}$) é uma função não-linear do número efetivo de migrantes ($N_em$). Ver Whitlock & McCauley (1999).

12.7 Exercícios

12.7.1 Exercício 1 – Duas subpopulações quaisquer

Suponha que existam duas subpopulações, $X$ e $Y$, com frequencias gênicas iniciais de um alelo $A$ iguais a $p_{0,X}=0.2$ e $p_{0,Y}=0.8$, respectivamente, sendo que $1\%$ dos indivíduos em uma subpopulação em qualquer geração são migrantes.

Desta forma, calcule a frequência alélica nas duas populações após…

… 5 gerações.
… 25 gerações.
… 100 gerações.

12.7.2 Exercício 2 – Aranha do deserto

Os indivíduos de uma espécie de aranha do deserto (Agelenopsis aperta) apresentam características comportamentais de base genética que os adaptam às pressões seletivas de diferentes ambientes:

As aranhas de terras áridas, com baixa pressão de predação e baixa disponibilidade de presas, são muito territoriais e não discriminam a presa.
As aranhas de floresta ribeirinha, com alta pressão de predação por pássaros e abundância de presas, são pouco territoriais e discriminam entre itens de presa com maior ou menor retorno energético.

Indivíduos de uma população de floresta ribeirinha do Arizona que é cercada por populações de áreas áridas, apresentam uma mistura de comportamentos de áreas áridas e ribeirinhas.

Esses comportamentos de áreas áridas podem ser considerados mal-adaptados a um ambiente ribeirinho, onde os locais de teia são abundantes, as presas são abundantes e as pressões de predação são altas.

Estaria o fluxo gênico mantendo esses comportamentos mal-adaptativos na população ribeirinha do Arizona?

Usando os dados abaixo de isoenzimas isoenzimas para cinco populações locais da aranha do deserto (uma população da floresta ribeirinha e quatro populações próximas de habitats mais áridos), obtidos por Riechert (1993):

Locus	$F_{ST}$
PGI1	0.020
PGM1	0.023
EST1	0.021
MDH2	0.032
IDH1	0.019
GOT2	0.031
αGPD1	0.029
SOD1	0.145
LDH1	0.012
MDH1	0.141
GAM1	0.063
HEX1	0.034
GOT1	0.033
FUM2	0.129

O que pode-se concluir?

Notas de Aula em
Genética de Populações