Capítulo 13 Mutação

Figura 13.1: Os padrões de polimorfismo de proteínas vistos na natureza são consistentes com a visão de que a maioria dos polimorfismos e diferenças fixas entre as espécies são fortemente deletérios ou seletivamente neutros. Esta proposta foi chamada de teoria neutra da evolução molecular. Retirado de Casillas & Barbadilla (2017)

Kimura 1968. doi: 10.1038/217624a0

Ohta 1973. doi: 10.1038/246096a0

A mutação é uma força evolutiva uma vez que promove uma mudança nas frequências gênicas ao longo do tempo.

Por exemplo, considere uma população com de tamanho \(N = 1000\) indivíduos, todos homozigotos em um locus gênico com o alelo \(A\).

Uma mutação que ocorra em um desses alelos, produzindo um único novo alelo \(a\), mudará a frequência \(p\) do alelo \(A\) de uma geração \(t\) para a outra \(t+1\) , onde:

\[p_t = \frac{2N}{2N} = 1 \]

e

\[ p_{t+1} = \frac{2N-1}{2N} = 0.9995\]

Evidentemente, esta é uma mudança muito pequena, mas ainda assim é uma mudança evolutiva.

A mutação é a fonte última de toda a variação genética, pois é ela que introduz novos alelos em uma população.

Embora a evolução não seja possível sem as mutações, a evolução não é simplesmente o acúmulo de mutações ao longo do tempo.

A mutação, por si só, introduz novas variantes genéticas em uma população, o que não é possível de promover grandes mudanças gênicas ao longo do tempo evolutivo.

Outras forças evolutivas (i. e., seleção, deriva, e fluxo gênico) atuam sobre variantes mutantes, fazendo com que a mudança nas frequências alélicas seja mais expressiva.

<br.

13.1 Modelando as mutações

Modelos de mutação são caracterizações conceituais de como o processo de mutação resulta no desenvolvimento de novos estados alélicos.

Neste ponto, não leva-se em conta as conseqüências de adaptabilidade dessas alterações.

13.1.1 Mutação direta

Considere o modelo mais simples de mutação, no qual um alelo \(A\) em um dado locus tem a chance de se transformar em um alelo \(a\) a cada geração.

Esta é a única forma de mutação possível neste modelo (apenas um alelo mutante), e a mutação é irreversível (um alelo \(a\) não pode sofrer mutação de volta para um alelo \(A\)).

A chance desta mutação acontecer depende da taxa de mutação geracional \(\mu\), onde:

\[ A \overset{\mu}{\rightarrow} a\]

Como a mutação é aleatória, essa taxa representa a probabilidade de mutação por locus por geração. Assim, embora o número real de mutações em qualquer geração possa variar em quantidade, a taxa de mutação é uma estimativa da probabilidade média de aparecimento de mutações durante longos períodos de tempo.

Logo, de uma geração \(t_0\) para a outra \(t_1\), assumindo que \(f(A, t_0) = p_0\) e $ f(a, t_0) = q_0$, e $ f(A, t_1) = p_1$ e $ f(a, t_1) = q_1$,teremos:

\[ p_1 = p_0(1- \mu)\]

e

\[ q_1 = q_0 + p_0 \mu\]

Na segunda geração, se a taxa de mutação \(\mu\) é constante, teremos que:

\[ \begin{aligned} p_2 &= \color{red}{p_1}(1- \mu) \\ &= \color{red}{p_0(1- \mu)}(1- \mu) \\ &= p_0(1- \mu)^2 \\ &= p_0 - 2p_0\mu + p_0\mu^2 \end{aligned} \]

e

\[ \begin{aligned} q_2 &= \color{blue}{q_1} + \color{red}{p_1} \mu \\ &= \color{blue}{q_0 + p_0 \mu}+\color{red}{p_0(1- \mu)} \mu \\ &= \color{green}{q_0} + 2p_0\mu - p_0\mu^2 \\ &= \color{green}{1-p_0} + 2p_0\mu - p_0\mu^2 \\ &= 1 - \left( p_0 - 2p_0\mu + p_0\mu^2 \right) \\ &= 1 - p_2 \end{aligned} \]

Figura 13.2: NO modelo de mutação direta, a taxa de mutação geracional \(μ\) promove o aumento do alelo \(a\) em detrimento do alelo \(A\).

Assim, após \(t\) gerações de mutações com taxa \(\mu\),

A frequencia \(p_t\) do alelo \(A\) será:

\[ p_t = p_0 \left( 1 - \mu \right)^t \]

E a frequencia \(q_t\) do alelo \(a\) será:

\[ q_t = 1 - p_t\]

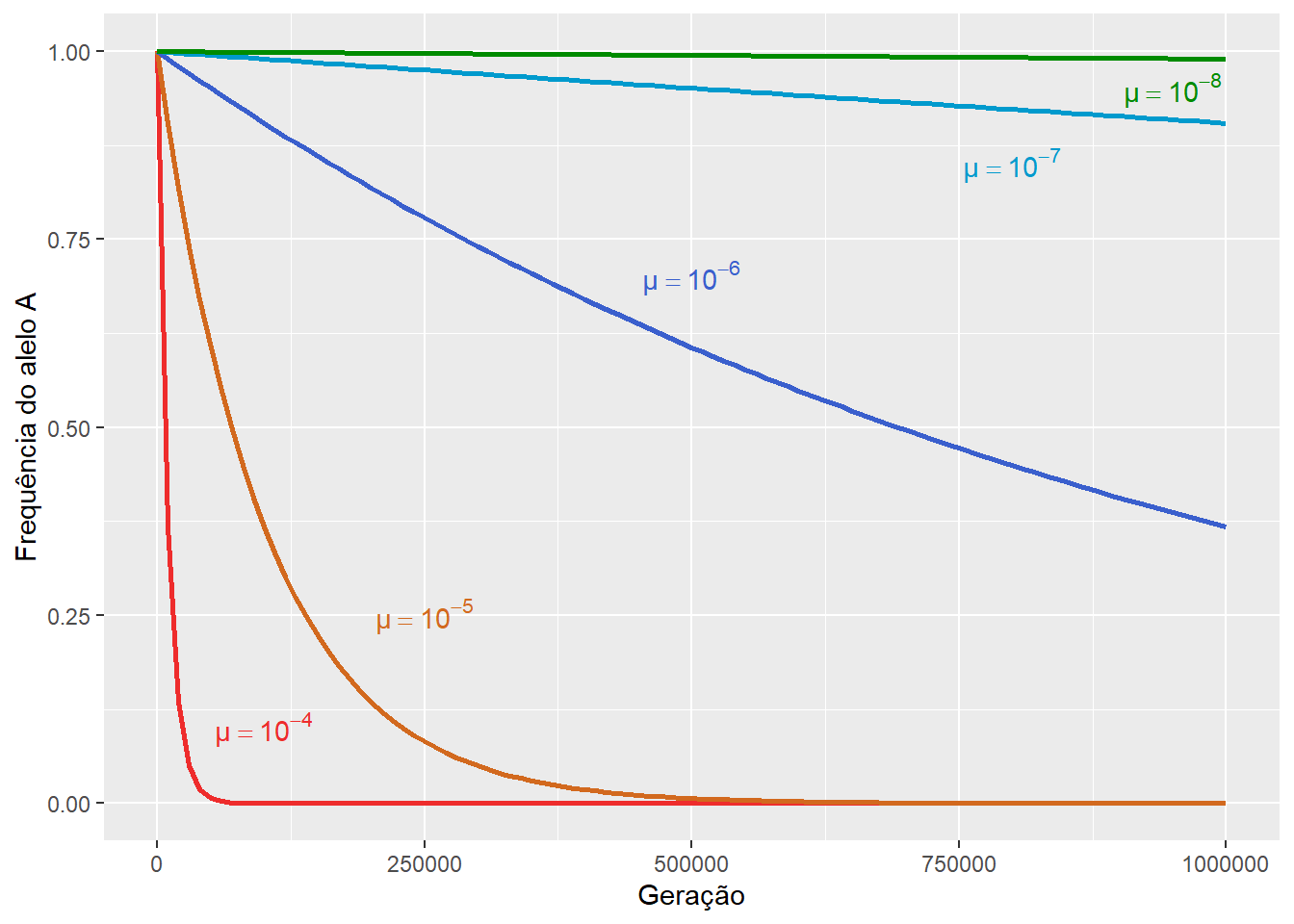
Figura 13.3: A mutação do alelo \(A\) para o alelo \(a\) promoverá uma mudança evolutiva cuja direção é a diminuiçãao da frequência alélica \(p\), e aumento da frequência alélica \(q\), proporcionalmente à taxa de mutação \(μ\).

13.1.2 Mutaçao reversa

Sob um modelo de mutação reversível, além das mutações do alelo \(A\) para a alelo \(a\), também há a ocorrência de mutações que transformam o alelo \(a\) de volta para o alelo \(A\).

Desta forma, para que ocorra mudança nas frequências alélicas de uma geração para outra, é necessário que as taxas de mutação de um alelo para o outro sejam diferentes uma da outra (balanço mutacional diferente de zero).

Sendo \(\mu\) a taxa de mutação do alelo \(A\) para um alelo \(a\), temos também agora a probabilidade de um alelo \(a\) mutar para o alelo \(A\), que irá depender de uma nova taxa de mutação \(\nu\), de forma que:

\[A \mathrel{\mathop{\rightleftharpoons}^{\mu}_{\nu}} a\]

Logo, de uma geração \(t_0\) para a outra \(t_1\), assumindo que \(f(A, t_0) = p_0\) e $ f(a, t_0) = q_0$, e $ f(A, t_1) = p_1$ e $ f(a, t_1) = q_1$,teremos:

br>

\[ p_1 = p_0(1- \mu) + q_o \nu\]

e

\[ q_1 = q_0(1- \nu) + p_0 \mu\]

Sendo $ p_0(1- ) $ e $ q_0(1- ) $ a proporção dos alelos \(A\) e \(a\) respectivamente que não sofreram mutação, e $ p_0 $ e $ q_o $ a proporção de alelos \(A\) que, por mutação, viraram \(a\), e vice-versa.

Figura 13.4: NO modelo de mutação reversa, as taxas de mutação geracional \(μ\) e $ u$ promovem o surgimento de novos alelos de ambos of tipos, cujo balanço dependerá dessas taxas e das frequências dos alelos naquela geração.

13.1.3 Equilíbrio das taxas de mutação

Seja \(\Delta p\) a mudança evolutiva na frequência \(p\) do alelo \(A\) de uma geração \(t\) para a seguinte \(t+1\), teremos que:

\[ \begin{aligned} \Delta p &= p_{t+1} - p_t \\ &= p_t(1- \mu) + q_t \nu - p_t \\ &= p_t - p_t \mu + q_t \nu - p_t \\ &= q_t \nu - p_t \mu \end{aligned} \]

Ou seja, no modelo de mutação reversa, a mudança evolutiva dependerá do balanço entre a proporção de alelos perdidos pela mutação direta (e. g., $ A a$) e de alelos criados pela mutação reversa (e. g., $ A a$).

A mudança evolutiva geracional na frequência do alelo \(A\) pode ser determinada independentemente da frequência do alelo \(a\) uma vez que \(p+q=1\), de forma que:

\[ \begin{aligned} \Delta p &= p_{t+1} - p_t \\ &= p_t(1- \mu) + \color{red}{q_t} \nu - p_t \\ &= p_t(1- \mu) + \color{red}{(1-p_t)} \nu - p_t \\ &= p_t - p_t \mu + \nu - p_t \nu - p_t \\ &= \nu - p_t \mu + - p_t \nu \\ &= \nu - p_t (\mu + \nu) \end{aligned} \]

Desta forma, é possível verificar que a mudança evolutiva dependerá da magnitudade da taxa de mutação “criadora” do alelo e das taxas globais de mutação que atuam modificando a frequência daquele alelo.

Dada a magnitudade das taxa de mutação direta e reversa, \(\mu\) e \(\nu\), e das freqüências alélicas na população, é possível que haja um balanço nulo entre a quantidade de alelos “criados” e “destruídos” por mutação em uma geração, e assim, a frequência \(p\) de um determinado alelo tenda a uma freqüência \(\hat{p}\) de equilíbrio, onde:

\[ \hat{p} = p_{t+1} = p_t \]

Uma população que atinja tal equilíbrio entre o aparecimento de mutações diretas e reversas, para todos os efeitos, não mais sofrerá mudança nas frequências alélicas, uma vez que:

\[ \Delta \hat{p} = 0 \]

Assim, é possível estimar a frequência de equlíbrio \(\hat{p}\) do alelo \(A\), pois embora as frequências alélicas estejam em equilibrio, este é um equilíbrio dinâmico dado o balanço das taxas de mutação geracional, onde:

\[ \Delta \hat{p} = \nu - \hat{p} (\mu + \nu) \]

E desta forma, teremos que:

\[ \nu - \hat{p} (\mu + \nu) = 0 \]

\[\hat{p} (\mu + \nu) = \nu \]

\[\hat{p} = \frac{\nu}{(\mu + \nu)} \]

Similarmente, a frequência de equlíbrio \(\hat{q}\) do alelo \(a\) será:

\[\hat{q} = \frac{\mu}{(\mu + \nu)} \]

Assim, no modelo de mutação reversa, a frequência de equlíbrio de um alelo será a razão entre a taxa de formação daquele alelo e a taxa global de mutação atuando sobre aquele alelo.

Note que $ $, quando $ $.

Note também que, no equilíbrio:

\[ \Delta \hat{p} = 0 = \hat{q} \nu - \hat{p} \mu\]

Logo, as frequências alélicas de equilíbrio se manterão proporcionais às taxa relativas de mutação direta e reversa, de forma que:

\[ \hat{q} \nu - \hat{p} \mu = 0 \]

\[\hat{p} \mu = \hat{q} \nu \]

\[\frac{\mu}{\nu} = \frac{\hat{q}}{\hat{p}} \]

E dado que \(\hat{p} + \hat{q} = 1\) …

• … a frequência de equlíbrio \(\hat{p}\) do alelo \(A\) será:

\[\hat{p} + \color{red}{\hat{q}} = 1\]

\[\hat{p} + \color{red}{\frac{\hat{p}\mu}{\nu}} = 1\]

\[\hat{p} \left( 1 + \frac{\mu}{\nu} \right) = 1\]

\[\hat{p} = \frac{1}{\left( 1 + \frac{\mu}{\nu} \right)}\]

• … e a frequência de equlíbrio \(\hat{q}\) do alelo \(a\) será:

\[\hat{q} + \color{red}{\hat{p}} = 1\]

\[\hat{q} + \color{red}{\frac{\hat{q}\nu}{\mu}} = 1\]

\[\hat{q} \left( 1 + \frac{\nu}{\mu} \right) = 1\]

\[\hat{q} = \frac{1}{\left( 1 + \frac{\nu}{\mu} \right)}\]

13.1.4 Mutações ao longo do tempo

Após \(t\) gerações de mutações reversíveis, com taxas \(\mu\) e \(\nu\), teremos que…

• … a frequencia \(p_t\) do alelo \(A\) será:

\[ p_t = p_{t-1} \left( 1 - \mu \right) + \left( 1 - p_{t-1} \right) \nu\]

• … a frequencia \(q_t\) do alelo \(a\) estimada apartir dessa, de forma que:

\[ q_t = 1 - p_t \]

Como a mudança evolutiva a cada geração dependerá do balanço entre as taxas formação de alelos dos dois tipos, uma função geral de que dependa somente das taxas de mutação e das frequências alélicas iniciais não é possível.

Contudo, na ausência de outras forças evolutivas, todas as populações sofrendo efeito de mutações reversíveis tenderão ao estado de equilíbrio.

Assim, sabendo o quanto falta para a população alcançar o equilíbrio, em termos da distância da freqüência alélica inicial da população da freqüência alélica de equilíbrio, e o quanto que as mutações conseguem ou não promover mudança evolutiva a cada geração, será possível estimar a frequência alélicas \(p\) em qualquer geração \(t\), de forma que:

\[ p_t = \frac{\nu}{(\mu + \nu)} + \left( p_0 - \frac{\nu}{(\mu + \nu)} \right) \left(1- \mu - \nu \right)^t\]

Onde \(\frac{\nu}{(\mu + \nu)}\) é a frequência de equilíbrio \(\hat{p}\), \(p_0\) é a frequência alélica inicial, quando \(t=0\), \(1- \mu - \nu\) é a proporção de alélos que não sofre mudança evolutiva por mutação, e \(t\) é o tempo em número de gerações decorridas.

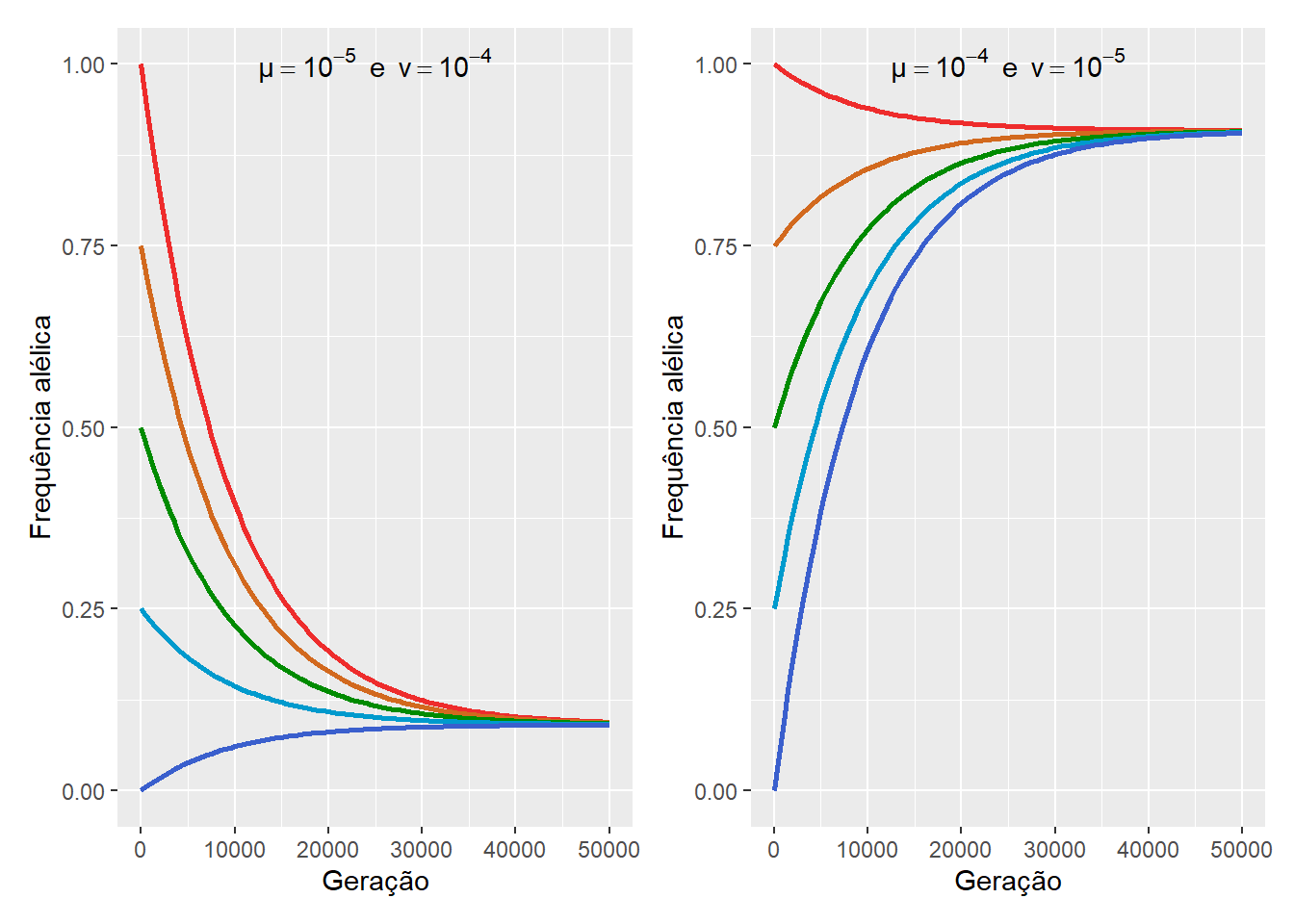
Figura 13.5: Na ausência de outras forças evolutivas, todas as populações sofrendo efeito de mutações reversíveis tenderão a um estado de equilíbrio.

13.2 Mutação e Endogamia

A endogamia será influenciada pelas taxas de mutação, uma vez que a mutação influenciará o nível de autozigosidade.

Se endogamia produzida de uma geração para outra é expressada como:

\[F_t = \frac{1}{2N_e} + \left( 1- \frac{1}{2N_e} \right)F_{t-1}\]

Com a ocorrência de mutações, o modelo de endogamia não será simétrico.

Assumindo que uma mutação irá alterar o estado dos alelos entregues para a próxima geração, com probabilidade \(\mu\):

• \((1 – \mu)\) – é a chance de que um alelo qualquer em uma geração não ter sofrido mutação, e

• \((1 – \mu)^2\) – é a chance de que nenhum dos dois alelos combinados em uma fecundação tenha sofrido mutação nessa geração.

Como somentes genótipos que não sofreram mutação podem produzir gametas autozigóticos, e portanto podem contribuir para o aumento da endogamia, podemos reformular a estimativa de endogamia esperada sob mutação, de forma que:

\[\hat{F} = \left[ \frac{1}{2N_e} + \left( 1- \frac{1}{2N_e} \right)\hat{F} \right] \left( 1-\mu \right)^2\]

Assim, enquanto o endocruzamento reduz a heterozigosidade, as mutações em populações endogâmicas irão promover o aumento da heterozigosidade, ao criar variantes alélicas de novo em genótipos previamente homozigotos em sua maioria, proporcionalmente à taxa de mutação \(\mu\).

Ao longo do tempo, espera-se que seja alcançado um equilíbrio na endogamia, promovido pelo antagonismo entre o endocruzamento e as mutações.

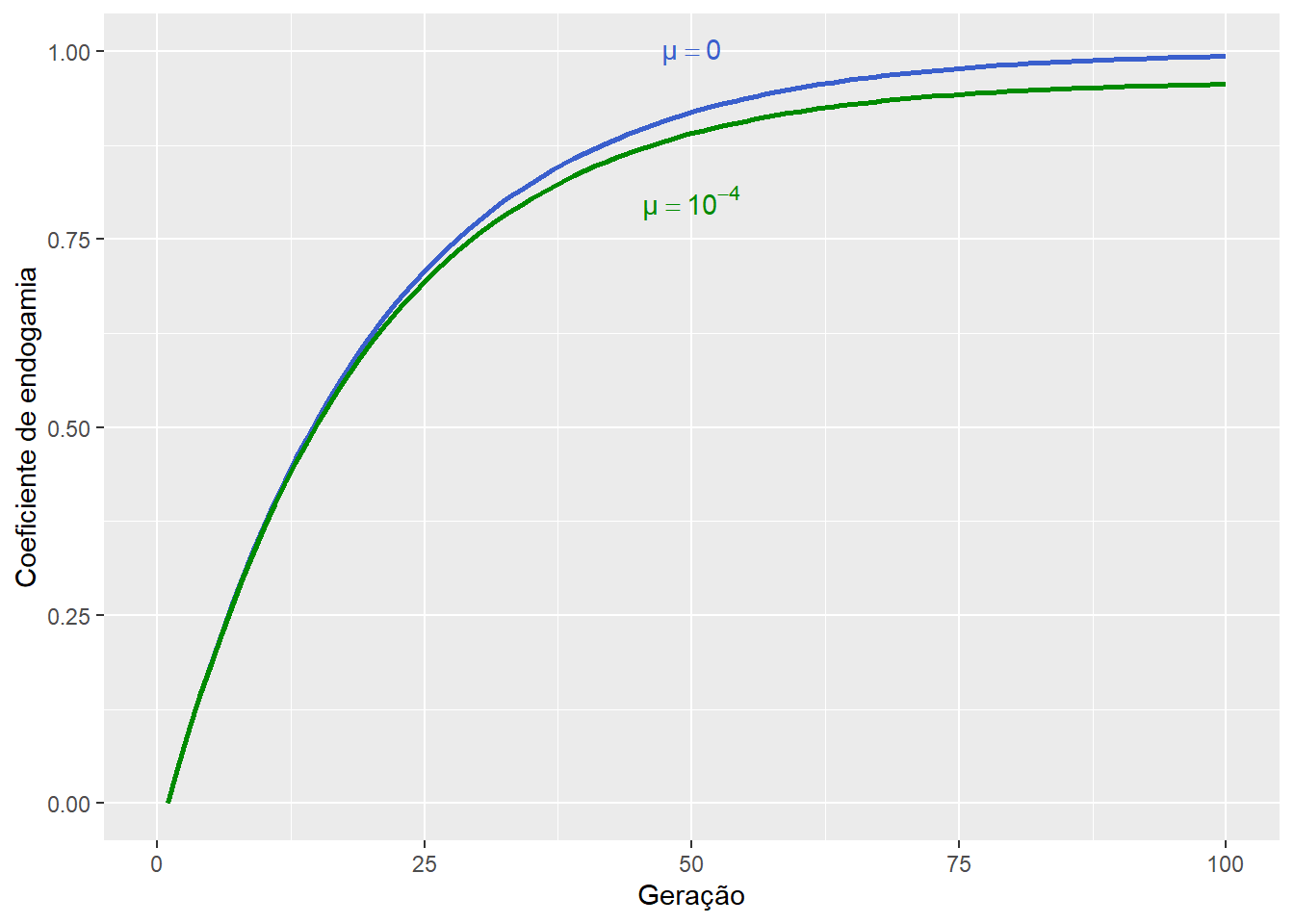
Figura 13.6: Uma vez que as mutações introduzem alelos novos na população, a probabilidade de encontro de alelos idênticos por descendência será menor nessas populações, e a endogamia ao longo das gerações irá crescer em uma taxa menor do que se não houvesse mutações.

Dada a expectativa de equilíbrio em relação à endogamia com base no tamanho efetivo da população (\(N_e\)) e na taxa de mutação (\(\mu\)) podemos verificar o nível de endogamia no equilíbrio (\(\hat{F}\)) como:

\[ \hat{F} = F_{t} = F_{t-1}\]

E assim, no equilíbrio:

\[ \Delta \hat{F} = 0\]

Assintoticamente à taxa de mutação \(\mu\), i. e., assumindo que o valor de \(\mu\) é pequeno o suficiente para que \(\mu^2 \sim 0\), teremos que:

\[ (1 - \mu)^2 \sim 1-2\mu\]

E assim, após várias simplificações algébricas da equação anterior (veja [aqui][#Provas]), teremos que:

\[\hat{F} \sim \frac{1-2\mu}{4N_e\mu+1-2\mu} \]

Desde que \(2\mu \ll N_e\mu\) e \(2\mu \ll 1\), teremos a relação aproximada:

\[\hat{F} \sim \frac{1}{4N_e\mu+1} \]

Para organismos diplóides, $ 4N_e= $, que é a medida da variação genética molecular, e desta forma:

\[ \hat{F} \sim \frac{1}{1+\theta} \]

Como qualquer genótipo que não é homozigoto deve ser heterozigoto, a heterozigosidade no equilíbrio mutação-deriva (\(\hat{H}\)) pode ser definida como:

\[ \begin{aligned} \hat{H} &= 1 - \color{blue}{\hat{F}} \\ &= 1 - \color{blue}{\frac{1}{4N_e\mu+1}} \\ &= \frac{4N_e\mu}{4N_e\mu+1} \\ &= \frac{\theta}{\theta+1} \end{aligned} \]

13.3 Exercícios

13.3.1 Exercício 1 – Elemento transponível mariner em Drosophila

Um fator genético descrito para Drosophila mauritiana resulta na deleção espontânea do elemento transponível mariner a uma frequência de aproximadamente 1% por geração para cada cópia (Hartl, 2001). Em uma população contendo um sítio autossômico no qual uma inserção mariner está fixada, quantas gerações seriam necessárias para que a frequência de moscas homozigotas para a deleção fosse maior do que 5%?

13.3.2 Exercício 2 – Componente flagelar em Salmonella

A bacteria Salmonella enterica possui um mecanismo de controle genético que regula a produção de duas formas alternativas de um componente proteico do flagelo celular, controladas por dois alelos: \(A\), para o componente flagelar de “fase específica”, e \(a\), para o componente flagelar de “fase de grupo”. A mudança de \(A \to a\) tem uma taxa de mutação de \(\mu = 8.6 \times 10^{-4}\) por geração, e a mudança de \(a \to A\) tem uma taxa de mutação \(\nu = 4.7 \times 10^{-3}\) por geração.

Note que essas taxas são ordens de magnitude maiores do que as taxas de mutação tipicamente observadas em outros genes. A razão é que as mudanças \(A \leftrightharpoons a\) não resulta de uma mutação no sentido convencional, mas de uma recombinação intracromossômica, como demonstrado por Simon e colaboradores (1980). Em termos formais, entretanto, podemos tratar esse sistema como um que permite mutação reversível.

Stocker (1949) estabeleceu culturas destas bactérias com frequências do alelo \(A\) igual a \(p_0 = 0\), e verificou que sua frequência aumentou para \(p_{30} = 0.16\) e para \(p_{700} = 0.85\). Quando cultivou bactérias com frequências do alelo \(A\) igual a \(p_0 = 1\), a frequência do alelo diminui para \(p_{388} = 0.88\) e para \(p_{700} = 0.86\).

Com base nesses dados:

• Calcule a frequência de equilíbrio \(\hat{p}\) esperada para o alelo \(A\).

• O valores observados por Stocker (1949) concordam com os estimados a partir das taxas de mutações de Simon e colaboradores (1980)?

• Se partirmos de uma população homogênea para o componente flagelar de “fase específica”, quantas gerações \(t\) são necessárias transcorrer para que 5% da população apresente o componente flagelar de “fase de grupo”?

13.3.3 Exercício 3 – Variação genética em Drosophila

Ayala e Tracey (1974, estudando variantes proteícas por eletroforese em uma população caribenha de Drosophila willistoni, obtiveram as estimativas abaixo de frequências alélicas para os loci gênicos da adenilato quinase 1 (Adk-1), leucina amino peptidade 5 (Lap-5) e xantina desidrogenase (Xdh).

Alelo	Adk-1	Lap-5	Xdh
1	0.574	0.801	0.446
2	0.309	0.177	0.406
3	0.114	0.014	0.092
4	0.003	0.004	0.034
5	-	0.004	0.014
6	-	-	0.004
7	-	-	0.002
8	-	-	0.002

Com base nesses dados, estime, para cada gene:

1. a homozigosidade;

2. a heterozigosidade esperada; e

3. a variação genética molecular (\(\theta\)).